INTRODUCTION

This lab is to analyze the implementation of the Kalman Filter through Python in Jupyter lab and then apply it on the robot. According to the instruction, the KF should be firstly initialized and then tuned with certain values to achieve best performance.

PRELAB

Parts Required

• 1 x R/C stunt car
• 1 x SparkFun RedBoard Artemis Nano
• 1 x USB cable
• 2 x Li-Po 3.7V 650mAh (or more) battery
• 2 x Dual motor driver
• 2 x 4m ToF sensor
• 1 x 9DOF IMU sensor
• 1 x Qwiic connector

LAB TASKS

Estimate drag and momentum

After receiving the data sent from the Artemis through BLE channel, the values of time, distance, pwm can be obtained and a certain fraction of the data array is tunked to be analyzed, by using the following code.

Therefore, the three figures can be obtained, indicating the motor input, distance and velocity along with the time.

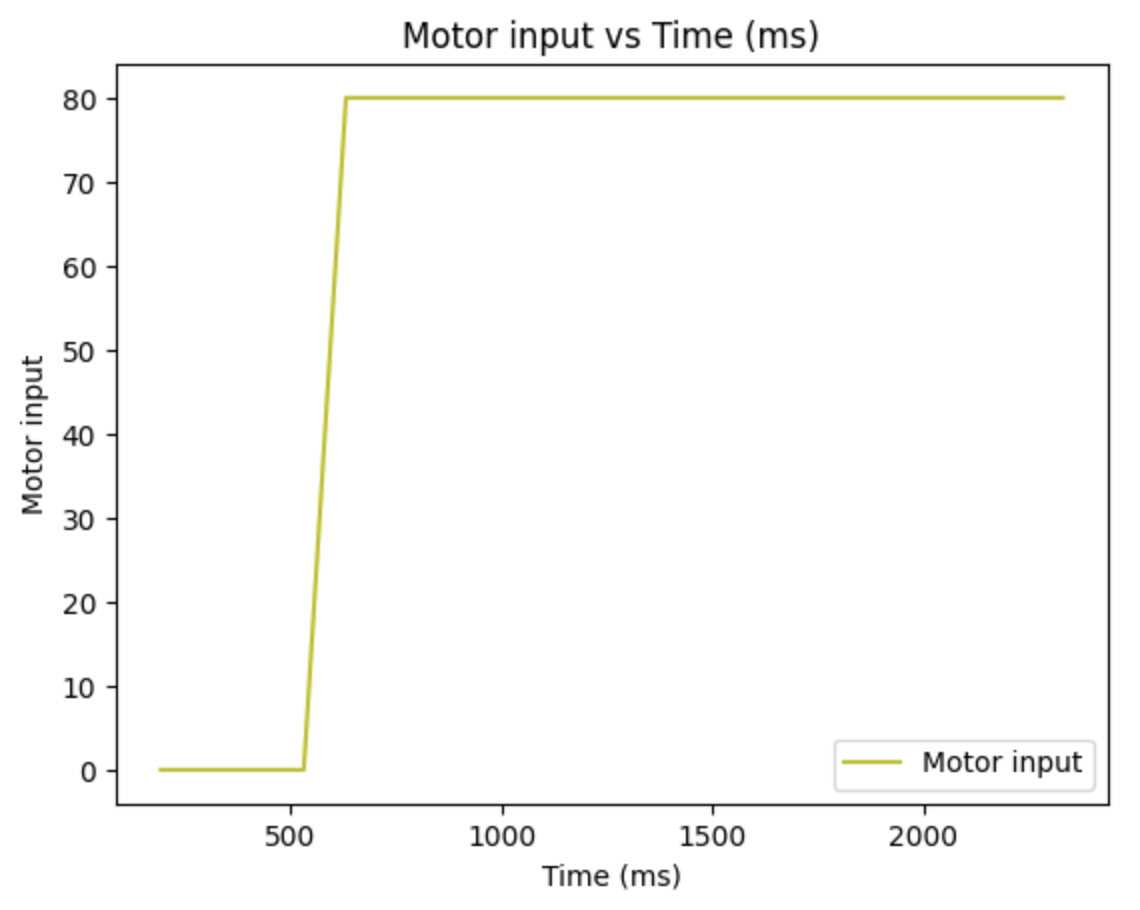
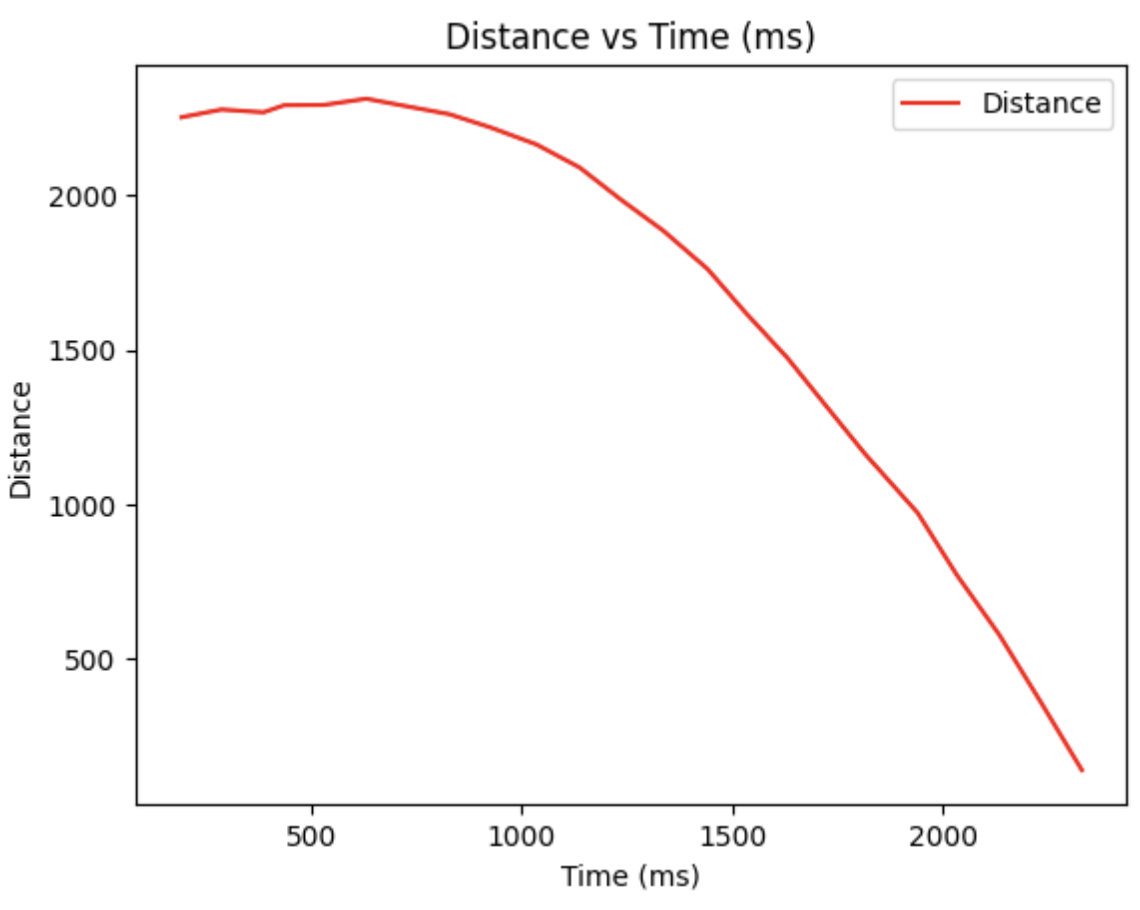
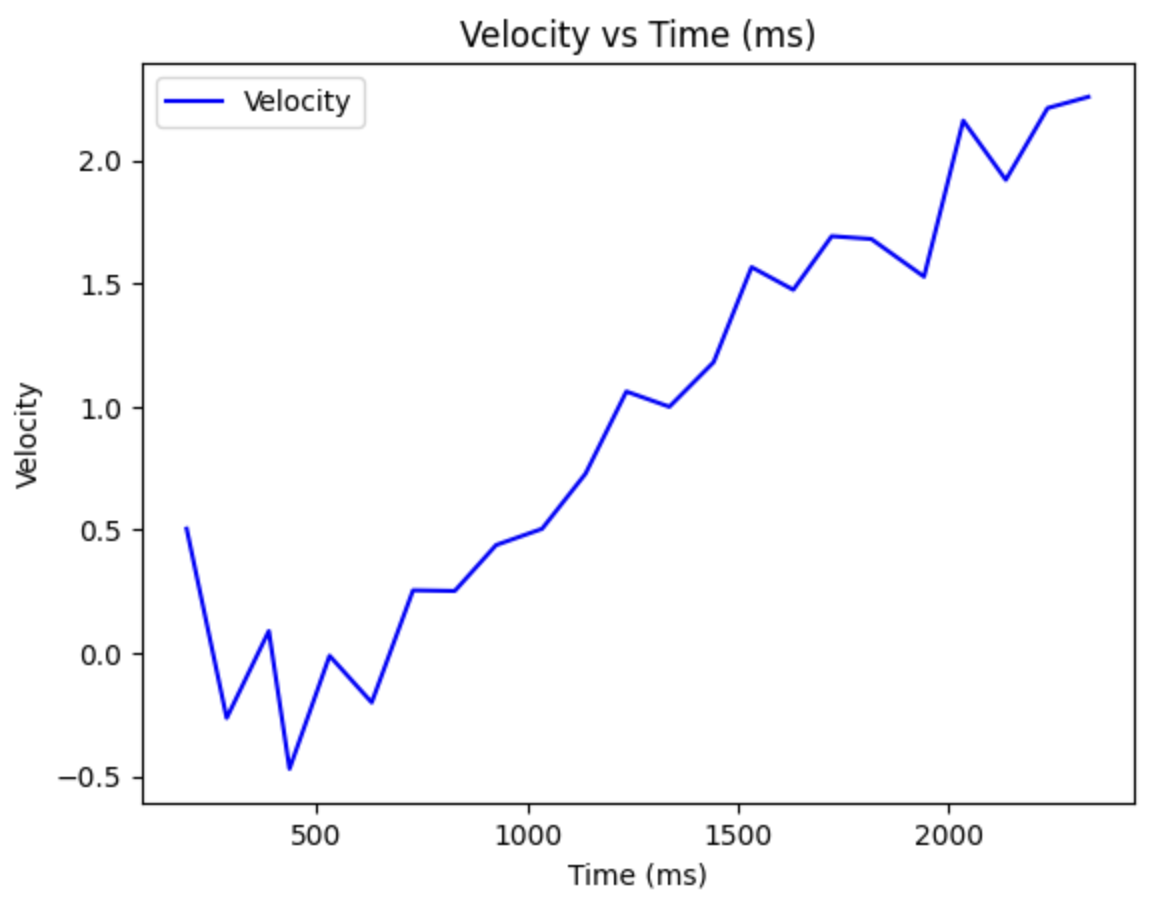
From the velocity digram, we can get time of reaching the steady state, which is around 1500ms, and the steady state speed is around 2258 mm/s. Thus, the following parameters can be initialized as below.

Where we get the value of d and m:

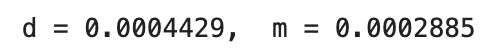
Initialize KF (Python)

With the data collected and parameters initialized, the KF filter can be set up according to the following instructions.

The image presented in the lecture slides illustrates the equations of the Kalman Filter. Various parameters need to be identified in the workflow: matrices A, B, C for creating the state space equation, along with noise matrices sigma_u and sigma_z.

The first step is to compute the A and B matrix. Given the condition that the sampling frequency of TOF sensor is around 100ms, so the parameter detla_T is set to 0.1.

Hence, the A and B matrix can be obtain, which are shown in below:

Next, the C matrix can be determined and it is a m x n matrix, where n are the dimensions in your state space, and m are the number of states you actually measure. Therefore, the C matrix is [-1,0], since the distance is represented from negative to 0 as the robot approaching the wall. Furthermore, the state vector, X should also be initialized by the following code.

Furthermore, the noise covariance matrices are determined. The parameter sigma_u depends on the sampling rate. The two standard deviations, sigma1 and sigma2, represent the confidence in the modeled position and speed, respectively. We utilize a diagonal matrix because we assume that these variables are uncorrelated. Also, sigma3 is defined as 20.

Currently, ballpark numbers for the variance only have rough values, and later it will be tested and tuned to best value.

Implement and test Kalman Filter in Jupyter (Python)

Firstly, the Kalman Filter function is defined as following, and the data through KF filter is stored in the array, kf_data. Moreover, the filtered data is extracted out.

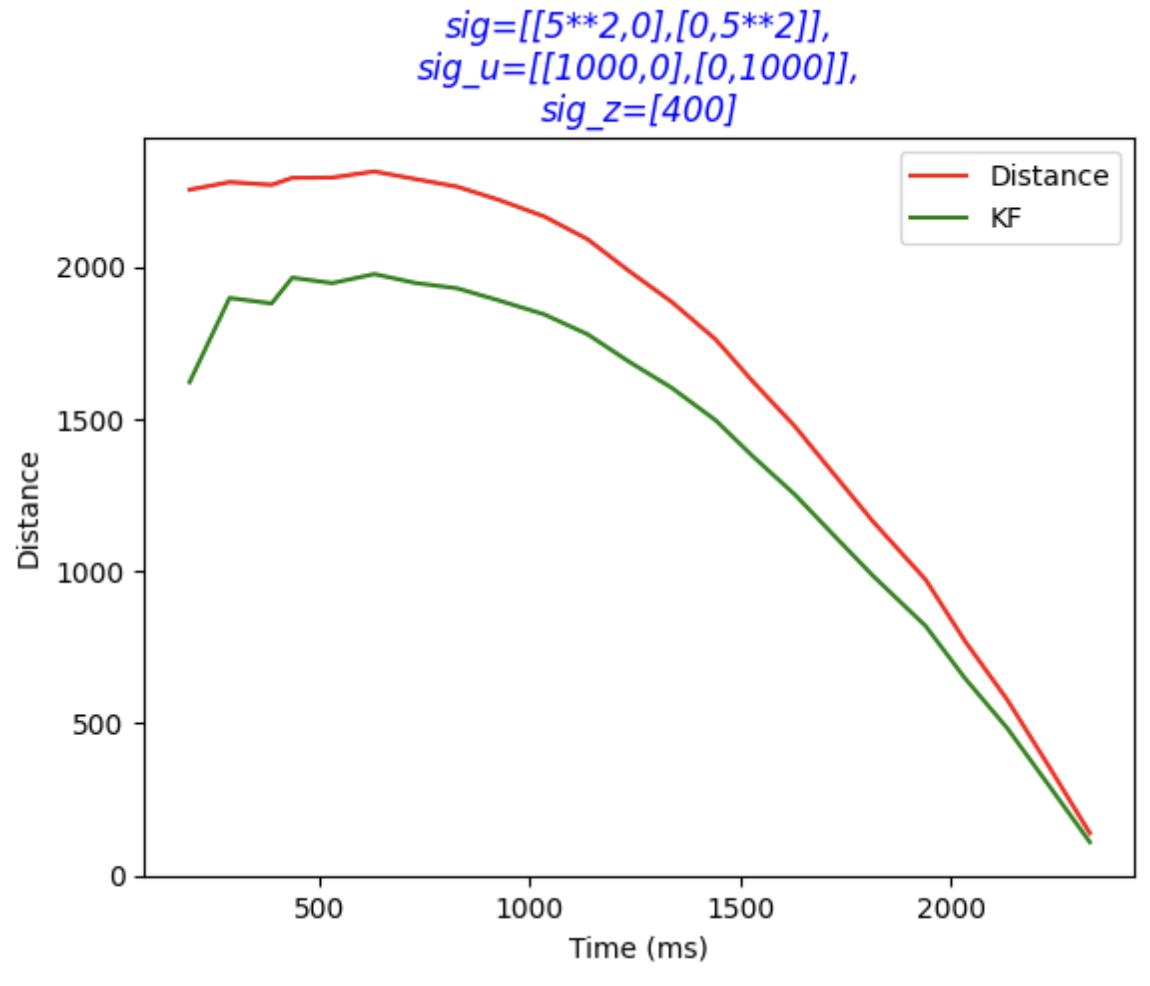
Therefore, the original and the filtered data are both plot in the figure, with the parameters of sig=[[5**2,0],[0,5**2]],sig_u=[[1000,0],[0,1000]],sig_z=[400].

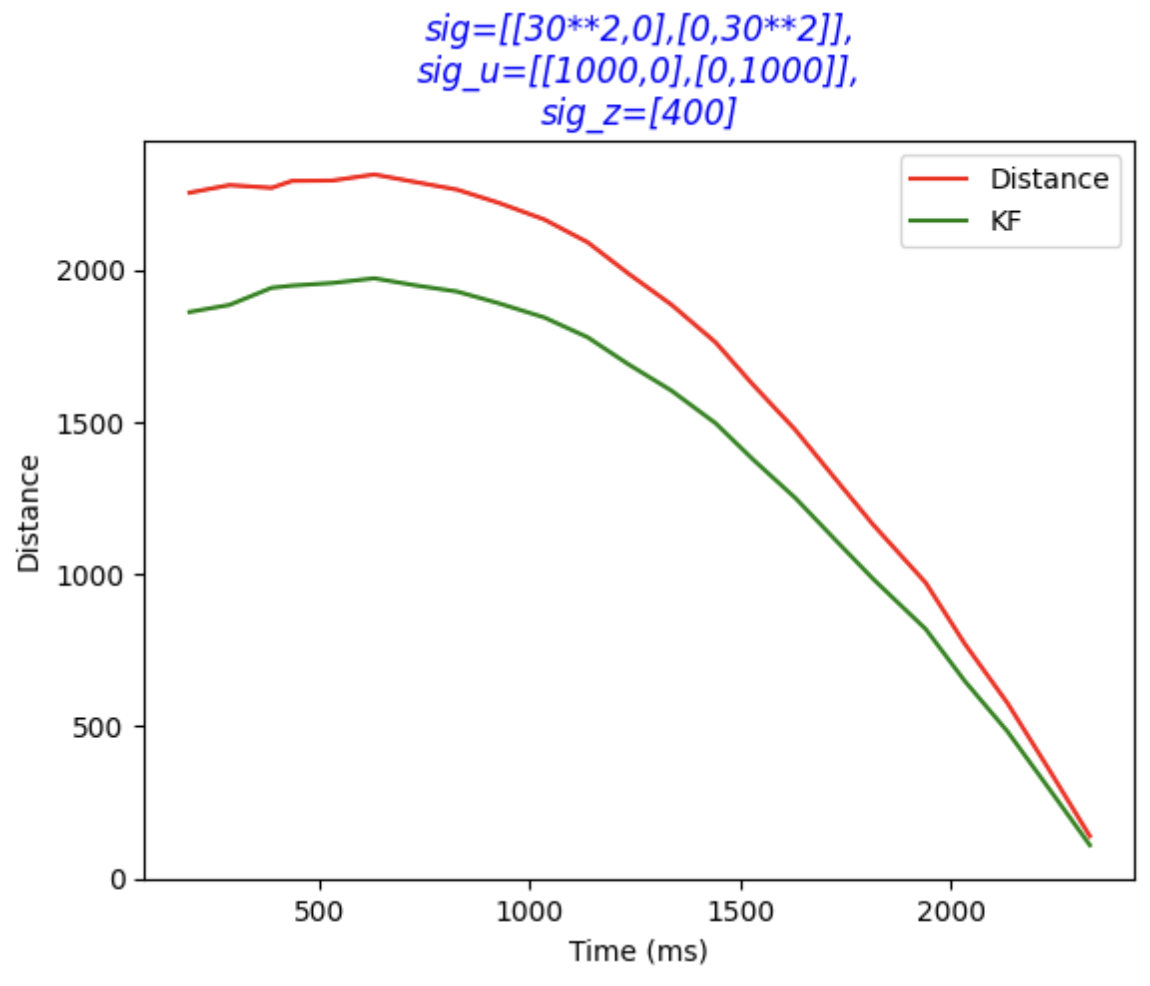
And them the paramter of sig is modified as below and we get a new figure, where the filtered data is smoother.

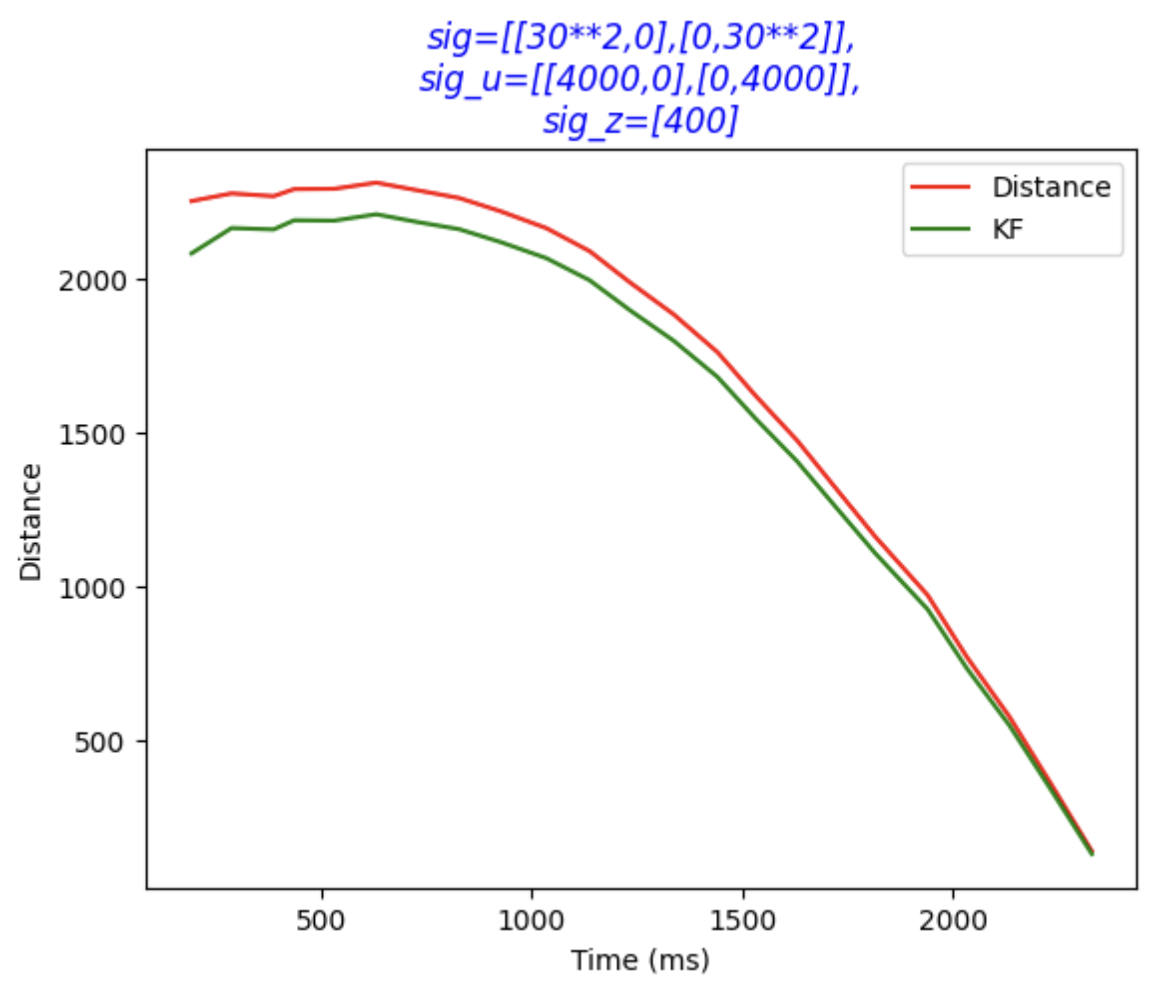
Next, the value of sigma1, sigma2 are changed as below, and it is indicated in the figure that those two array values are getting closer to each other.

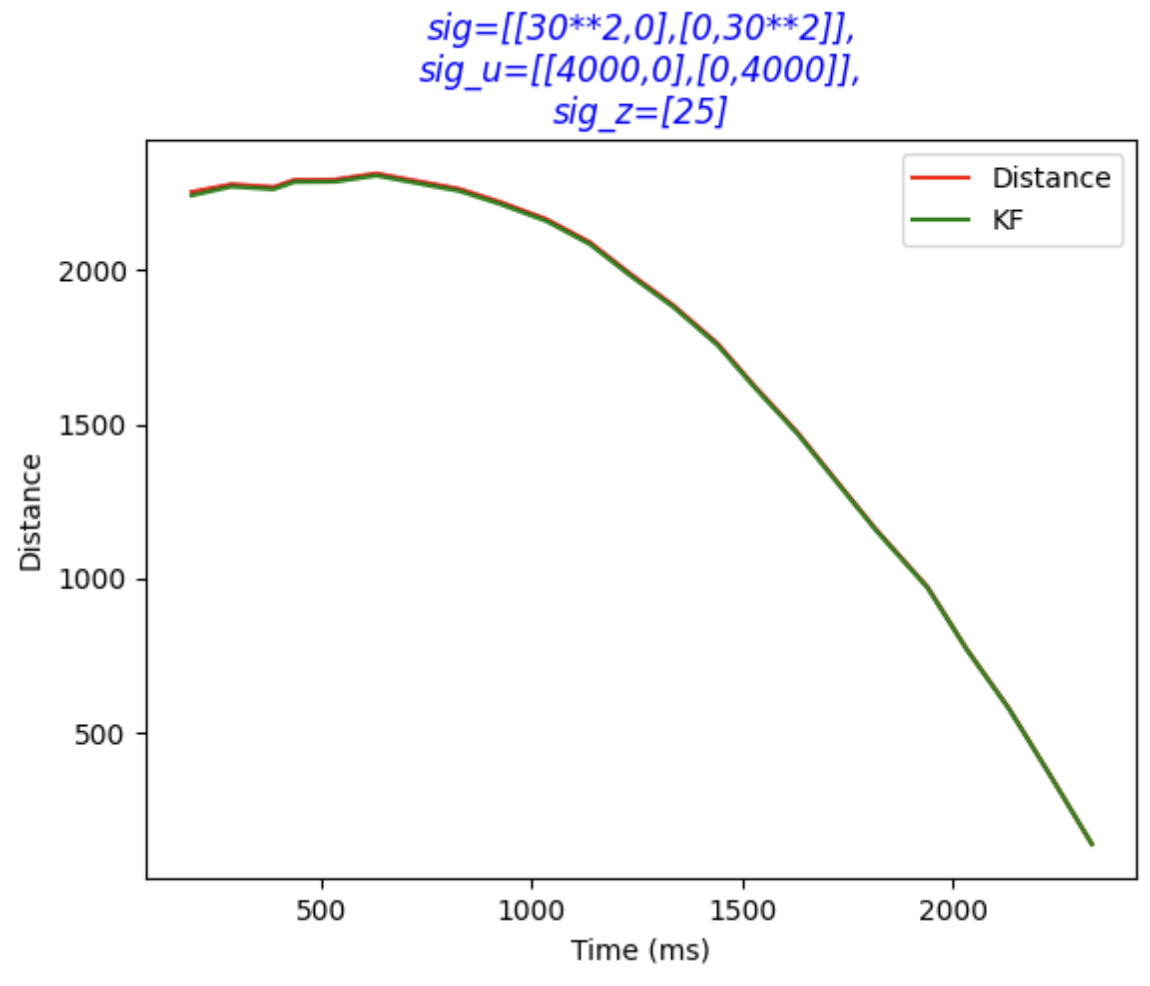
Finally, sigma3 is adjusted accordingly, and we obtain the data with KF, which is approximately overlap with the original record.

Kalman filter at a faster frequency

I have also modify the sampling rate to make the KF run at a faster frequency. Consequently, when delta_T = 0.1/5, 20ms. In between readings, the prediction step is used to estimate the state of the car, which is similar to the linear extrapolation step from lab 6, but the prediction step is used of the Kalman filter instead.

Therefore, we obtain the figure as below, which illustrates the diagram with decreasing delta_T.

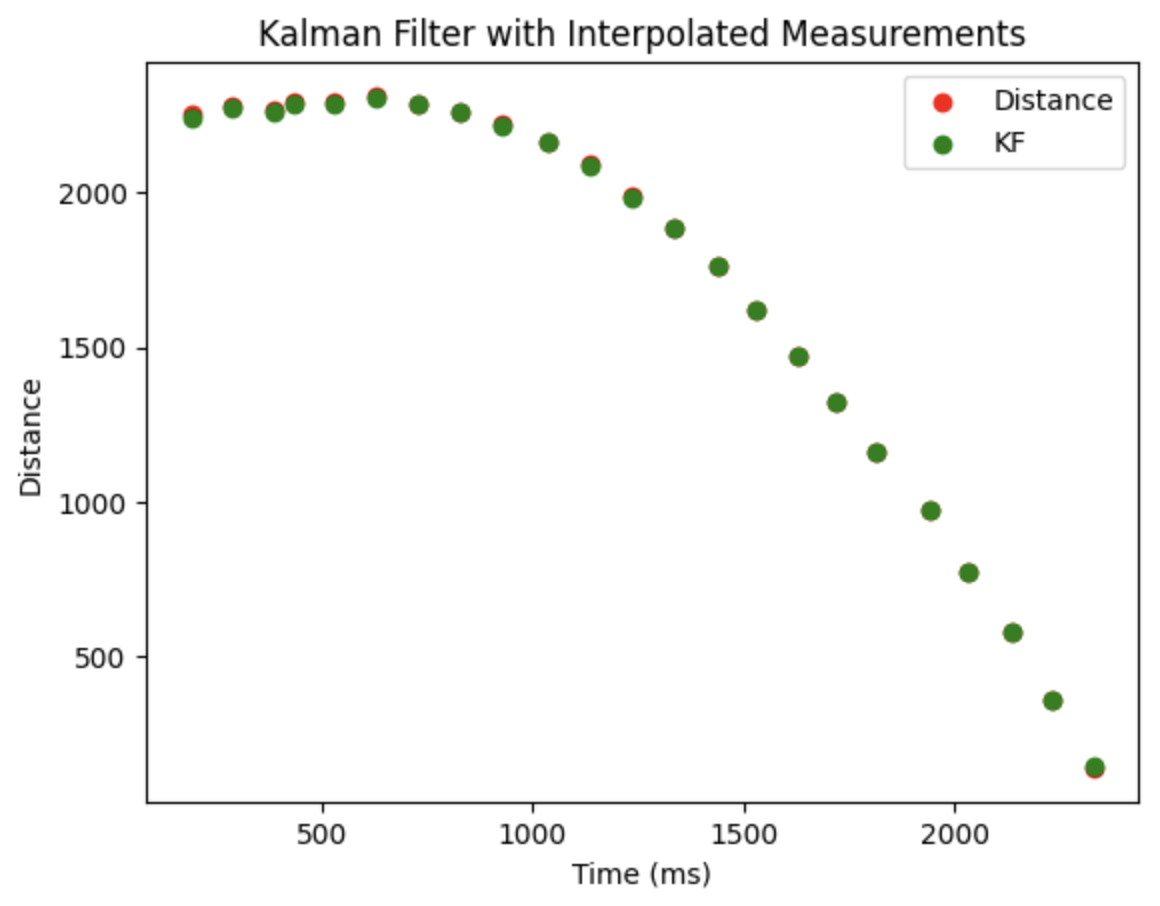
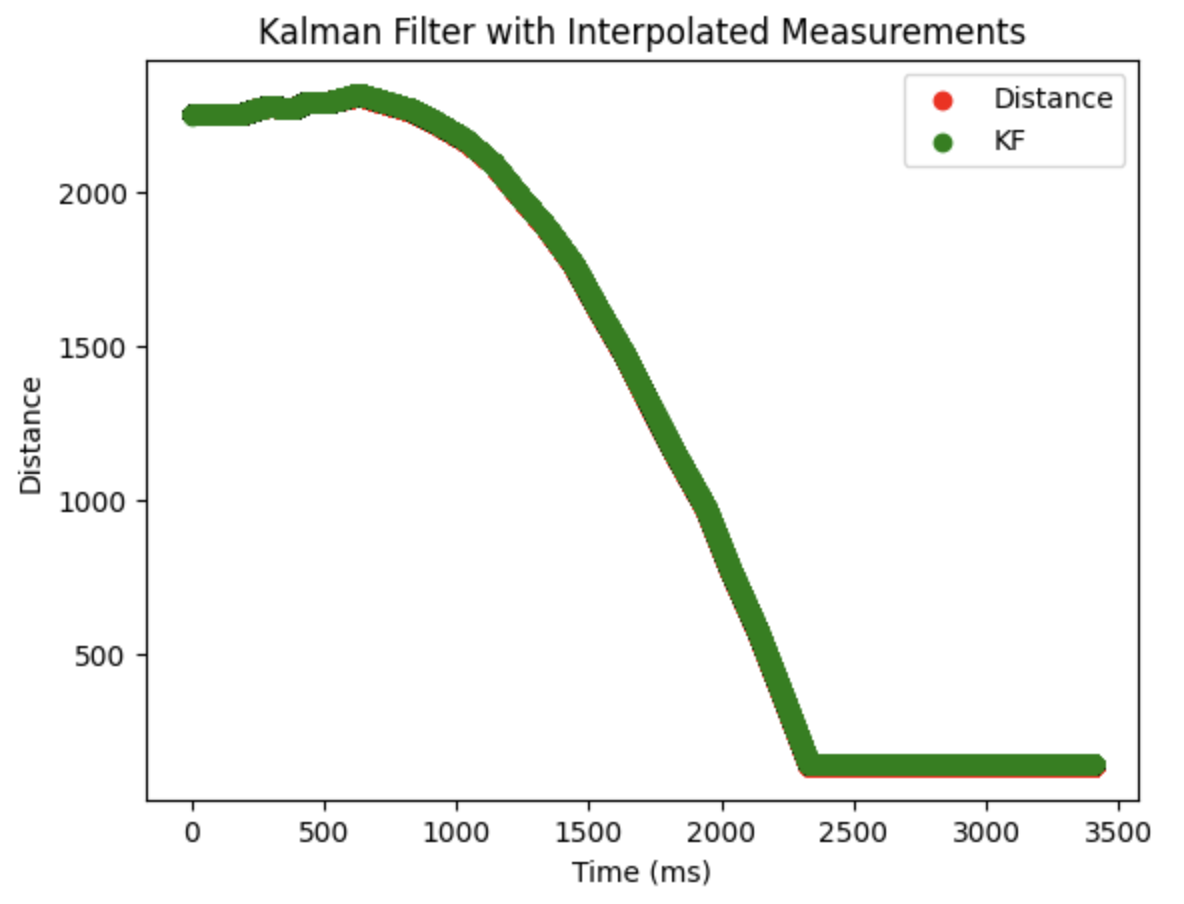
Implement on robot

Finally, the KF is implemented on the robot, where the parameters are initialized with the following setup.

Where we apply the function KF() in the PID control function.

And we obtain the TOF data with and without Kalman Filter.

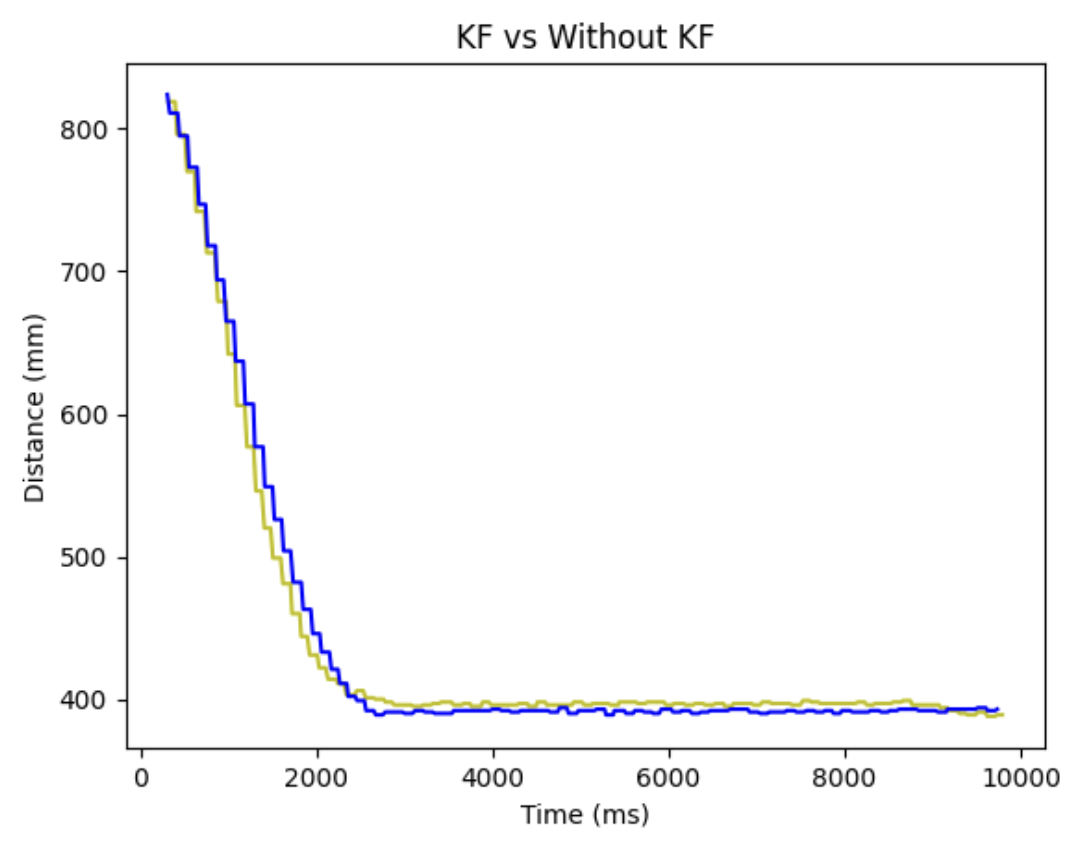
DISCUSSION

This lab is to learnt the performance of the Kalman Filter and access the effectiveness, which is beneficialthe navigation and prediction of the recorded data.